А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'Т':
Любые две простые равновеликие фигуры на плоскости (в том числе, например, равновеликие многоугольники) равносоставлены.
См. "равносоставленные фигуры"
и задачу 105196.
Диагонали описанного шестиугольника пересекаются в одной точке.
(См. задачи 56729,58450.)
Рассмотрим четырехугольник ABCD. Пусть u = AD2, v = BD2, w = CD2,
U = BD2 + CD2 - BC2,
V = AD2 + CD2 - AC2,
W = AD2 + BD2 - AB2.
Теорема Гаусса утверждает, что
uU2 + vV2 + wW2 = UVW + 4uvw.
(См. задачу 57697.)
Пусть прямые AA1, BB1 и CC1 пересекаются в одной точке O.
Теорема Дезарга утверждает, что в этом случае точки пересечения (если они есть) прямых
AB и A1B1, BC и B1C1, AC и A1C1 лежат на одной прямой.
* Теорема Дезарга проективно двойственна теореме Паппа.
Правильный тетраэдр и куб того же объема не равносоставлены.
См. "равносоставленные фигуры".
Перпендикуляры, опущенные из
точек
A1, B1, C1 на стороны BC, CA, AB треугольника ABC,
пересекаются в одной точке тогда и только тогда, когда
A1B2 + C1A2 + B1C2 = B1A2 + A1C2 + C1B2.
(См. задачу 57169.)
Пусть точки A, B, C, D, E и F лежат на одной окружности.
Тогда прямые Паскаля шестиугольников ABFDCE, AEFBDC и ABDFEC пересекаются в одной точке.
(См. задачу 58520.)
Квадрат стороны треугольника равен сумме квадратов двух других
его сторон без удвоенного произведения этих сторон на косинус угла между ними.
То есть, если a, b, c — стороны треугольника;
![]() — угол, противолежащий стороне a, то
— угол, противолежащий стороне a, то
Дан треугольник ABC. Некоторая прямая
пересекает его стороны AB, BC и продолжение стороны AC в точках
C1, A1, B1 соответственно. Тогда
Теорема Менелая часто используется для доказательства того, что точки пересечения некоторых
прямых лежат на одной прямой.
(См. задачи 53857,56898.)
Пусть начало координат является центром симметрии
выпуклой фигуры площадью более 4. Тогда эта
фигура содержит хотя бы одну точку с целыми координатами,
отличную от начала координат.
(См. задачу 58215.)
В треугольнике ABC проведены триссектрисы (лучи,
делящие углы на три равные части). Ближайшие к стороне BC
триссектрисы углов B и C пересекаются в точке A1;
аналогично определим точки B1 и C1 (см. рис.). Теорема Морли утверждает, что полученный треугольник A1B1C1 равносторонний.
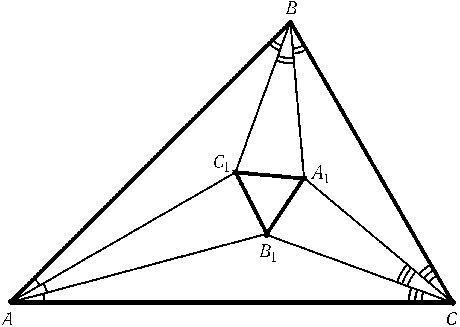
(См. задачу 56893.)
Если на сторонах правильного треугольника внешним (внутренним) образом построены
правильные треугольники, то их центры образуют правильный
треугольник.
* Отметим, что разность площадей треугольников, полученных при построении правильных
треугольников внешним и внутренним образом, равна площади исходного треугольника.
(См. задачи 55746,57960.)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Центр масс системы точек
останется прежним, если часть точек заменить одной точкой, которая расположена в их центре
масс и которой приписана масса, равная сумме масс удаленных точек.
(См. задачу 57748.)
Рассмотрим два треугольника ABC и A1B1C1
таких, что прямые AA1, BB1 и CC1 пересекаются в одной точке O,
и прямые AB1, BC1 и CA1 пересекаются в одной точке O1.
Тогда прямые AC1, BA1 и CB1 тоже пересекаются в одной точке O2
(См. задачу 58437.)
Рассмотрим четыре точки A, B,C, D.
Пусть P, Q, R — точки пересечения прямых AB и CD, AD и BC, AC и BD соответственно;
K и L — точки пересечения прямой QR с прямыми AB и CD
соответственно. Тогда (QRKL) = - 1, где (QRKL) — двойное отношение точек Q, R, K, L.
(См. задачу 58437.)
Параллельные прямые, пересекающие стороны угла, отсекают от сторон
угла пропорциональные отрезки.
Сумма углов треугольника равна
180o.
Рассмотрим два треугольника ABC и A1B1C1 таких,
что прямые AA1, BB1 и CC1 пересекаются в одной точке O,
прямые AA1, BC1 и CB1 пересекаются в одной точке O1
и прямые AC1, BB1 и CA1 пересекаются в одной точке O2.
Тогда прямые AB1, BA1 и CC1 также пересекаются в одной точке O3.
(См. задачу 58438.)
Рассмотрим две прямые, на одной из которых взяты точки A1, B1 и C1, а на
другой — точки A2, B2 и C2. Пусть прямые A1B2 и A2B1, B1C2
и B2C1, C1A2 и C2A1 пересекаются в точках C, A
и B соответственно. Теорема Паппа утверждает, что тогда точки A, B и C лежат на одной
прямой.
* Теорема Паппа проективно двойственна теореме Дезарга.
(См. задачи 58435,58456.)
Точки пересечения противоположных сторон
(если эти стороны не параллельны) вписанного шестиугольника лежат на
одной прямой.
* Классическую формулировку теоремы Паскаля можно обобщить двумя способами. Во-первых, теорема будет верна не только для шестиугольника, но для произольной (возможно, самопересекающейся) шестизвенной ломаной с вершинами на окружности.
Во-вторых, теорема останется верна и если вместо окружности рассмотреть произвольную конику на плоскости.
(См. задачи 57105,58451,58519.)
Если прямая, не проходящая ни через одну из вершин треугольника, пересекает
одну из его сторон, то она пересекает ровно одну из двух других его сторон.
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов
катетов.
Если CD — высота прямоугольного треугольника ABC, проведённая
из вершины C прямого угла, то треугольники ABC, CBD и ACD — подобны.
Если при этом l, l1 и l2 — соответствующие отрезки этих треугольников, то
l2 = l12 + l22.
Если квадрат стороны треугольника равен сумме квадратов двух других сторон,
то треугольник прямоугольный. (
Рассмотрим точку X и правильный треугольник ABC. Из отрезков
XA, XB и XC можно составить треугольник, причем этот треугольник
вырожденный тогда и только тогда, когда точка X лежит на описанной окружности
треугольника ABC.
(См. задачу 57941.)
Для вписанного четырехугольника ABCD верно равенство:
AB . CD + AD . BC = AC . BD.
Рассмотрим окружности
![]() ,
,![]() ,
,![]() и
и ![]() , касающиеся данной
окружности в вершинах A, B, C и D выпуклого четырехугольника ABCD.
Пусть
T
, касающиеся данной
окружности в вершинах A, B, C и D выпуклого четырехугольника ABCD.
Пусть
T![]()
![]() — длина общей касательной к окружностям
— длина общей касательной к окружностям ![]() и
и ![]() (внешней, если оба касания внутренние или внешние одновременно,
и внутренней, если одно касание внутреннее, а другое
внешнее);
T
(внешней, если оба касания внутренние или внешние одновременно,
и внутренней, если одно касание внутреннее, а другое
внешнее);
T![]()
![]() , T
, T![]()
![]() и т. д. определяются аналогично. Тогда обобщенная теорема Птолемея
утверждает, что
T
и т. д. определяются аналогично. Тогда обобщенная теорема Птолемея
утверждает, что
T![]()
![]() T
T![]()
![]() + T
+ T![]()
![]() T
T![]()
![]() = T
= T![]()
![]() T
T![]()
![]() .
.
(См. задачу 57055.)
(См. задачу 57045.)
Пусть p, q и r —
натуральные числа, причем p, q![]() r. Тогда существует число
N = N(p, q, r), обладающее следующим свойством: если все
r-элементные подмножества N-элементного множества S
произвольным образом разбиты на два непересекающихся семейства
r. Тогда существует число
N = N(p, q, r), обладающее следующим свойством: если все
r-элементные подмножества N-элементного множества S
произвольным образом разбиты на два непересекающихся семейства ![]() и
и ![]() , то либо существует p-элементное подмножество множества S,
все r-элементные подмножества которого содержатся в
, то либо существует p-элементное подмножество множества S,
все r-элементные подмножества которого содержатся в ![]() , либо
существует q-элементное подмножество, все r-элементные
подмножества которого содержатся в
, либо
существует q-элементное подмножество, все r-элементные
подмножества которого содержатся в ![]() .
.
(См. задачу 58117.)
На плоскости дано конечное число точек, причем
такое, что любая прямая, проходящая через две из данных точек,
содержит еще одну данную точку. Тогда все данные точки лежат на одной прямой.
(См. задачу 58059.)
Стороны треугольника пропорциональны синусам противолежащих им углов. Более того,
если a, b, c — стороны треугольника; ![]() ,
, ![]() ,
, ![]() — противолежащие им углы, то
— противолежащие им углы, то
Если точка D расположена на стороне BC
треугольника ABC, то
AB2 . DC + AC2 . BD - AD2 . BC = BC . DC . BD.
(См. задачу 54717.)
На стороне BC треугольника ABC взята точка D. Окружность S1 касается
отрезков BE и EA и описанной окружности, окружность S2 касается отрезков
CE и EA и описанной окружности. Пусть I, I1, I2 и r, r1, r2
-- центры и радиусы вписанной окружности и окружностей S1, S2;
![]() =
= ![]() ADB. Тогда точка I лежит на отрезке I1I2, причём
I1I : II2 = tg2
ADB. Тогда точка I лежит на отрезке I1I2, причём
I1I : II2 = tg2![]() , причем
r = r1cos2
, причем
r = r1cos2![]() + r2sin2
+ r2sin2![]() (Тебо).
(Тебо).
(См. задачу 56705.)
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне
равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Окружность, проходящая через середины сторон (окружность девяти точек)
треугольника, касается его вписанной и трех вневписанных окружностей
(См. задачу 58348.)
Великая (или последняя) теорема Ферма утверждает, что уравнение
xn+yn=zn не имеет
отличных от нуля решений в целых числах при n>2 (n— натуральное число).
При n=2 уравнение имеет бесконечное количество целочисленных решений
(см. "пифагоров треугольник").
Великая теорема Ферма была сформулирована Пьером Ферма (1601—1665) на полях книги "Арифметика" Диофанта Александрийского. Сам Ферма привел доказательство своей теоремы (с помощью метода спуска) лишь для n=4. Для n=3 теорема была доказана Леонардом Эйлером в 1768 г. В дальнейшем теорема Ферма была доказана еще для ряда частных значений n. Полное доказательство Великой Теоремы Ферма было получено лишь в 1994 году английским математиком Эндрю Уайлсом.
Малая теорема Ферма утверждает, что если p— простое число,
и a— целое число, не кратное p, то ap-1-1
делится на p. В терминах сравнений это можно сформулировать так:
ap-1≡1 (mod p).
Если на плоскости имется n выпуклых фигур
(n ![]() 3), причем любые
три из них имеют общую точку, то и все n данных фигур имеют общую точку.
3), причем любые
три из них имеют общую точку, то и все n данных фигур имеют общую точку.
(См. задачу 58141.)
Теорема Шаля утверждает, что любое движение плоскости является одним из следующего списка:
параллельный перенос, поворот, скользящая симметрия (включая осевую). Теорема Шаля дает полную классификацию
всех движений плоскости.
* Часто также бывает удобно воспользоваться тем фактом, что любое движение плоскости есть композиция некоторого количества осевых симметрий (всегда можно обойтись не более, чем тремя).
*
Аналогичная теорема классифицирует все движения трехмерного пространства: всякое сохраняющее ориентацию движение
пространства является винтовым движением (то есть композицией поворота вокруг определенной оси с параллельным
переносом вдоль той же оси, причем как угол, так и вектор могут быть и нулевыми). Движение, меняющее ориентацию,
является композицией симметрии относительно плоскости и винтового движения.
(См. задачи 57904,57905.)
Пусть точки A1, B1 и C1
принадлежат соответственно сторонам BC, AC и AB треугольника ABC.
Отрезки AA1, BB1, CC1 пересекаются в одной точке тогда и
только тогда, когда
Теорему Чевы можно обобщить для случая, когда точки A1, B1 и C1 лежат не обязательно на сторонах треугольника, а лишь на прямых BC, AC и AB. Пусть k из этих точек лежит на сторонах треугольника и 3 - k — на продолжениях сторон. Пусть
Тогда прямые AA1, BB1 и CC1 пересекаются в одной точке или
параллельны тогда и только тогда, когда R = 1 и k нечетно.
(См. задачи 53856,56914.)
Теорема Чевы часто используется для доказательства того, что некоторые прямые пересекаются в одной точке.
см. "центральное проектирование".
Точкой
Жергонна называется точка пересечения прямых, соединяющих вершины треугольника с
точками касания вписанной окружности.
(См. задачу 53788.)
Точкой Лемуана треугольника называется
точка пересечения его симедиан.
Пусть четыре прямые расположены так ("в общем положении"),
что при их пересечении образуется четыре треугольника. Тогда описанные окружности этих треугольников
имеют общую точку, которая называется (точкой Микеля) этой конфигурации прямых.
*
Отметим, что центры описанных окружностей этих
треугольников лежат на одной окружности, проходящей через
точку Микеля.
(Cм. задачу 56628.)
Отрезки, соединяющие вершины треугольника с точками
касания вневписанных окружностей со сторонами, пересекаются в одной точке, которая
называется (точкой Нагеля) данного треугольника.
(Cм. задачу 56916.)
В литературе встречается три неэквивалентных определения точки Торичелли:
—
Построим на сторонах треугольника ABC
внешним образом правильные треугольники ABC1, AB1C и A1BC. Тогда
прямые AA1, BB1 и CC1 пересекаются в одной точке.
Эта точка называется точкой Торричелли данного треугольника.
(Cм. задачу 55735.)
См. также "изогонический центр".
— Точкой Торричелли называется точка, из которой все стороны треугольника видны под одинаковым углом (равным 120o). (Cм. задачу 55385.)
— Точка, лежащая внутри треугольника, для которой сумма расстояний от неё до вершин треугольника минимальна, называется точкой Торричелли. (Cм. задачу 55737.)
В случае треугольника, наибольший угол которого меньше 120o, все три определения задают одну и ту же точку. Если один из углов треугольника больше 120o, то точка, сумма расстояний от которой до вершин треугольника минимальна, совпадает с вершиной этого угла и отличается от точки, заданной первым определением. Точки, заданной вторым определением, в этом случае нет.
см. "изогонический центр".
Пусть на сторонах BC, CA и AB треугольника ABC взяты
точки A1, B1 и C1, причем прямые AA1, BB1 и CC1 пересекаются в одной точке P.
Тогда прямые AA2, BB2 и CC2, симметричные этим прямым относительно соответствующих биссектрис,
также пересекаются в одной точке Q.
В этом случае точки P и Q называются изогонально сопряженными относительно треугольника ABC.
((См. задачу 56924.)
Пусть прямые AP, BP и CP пересекают прямые BC, CA
и AB в точках A1, B1 и C1 соответственно, а точки A2, B2
и C2 выбраны на прямых BC, CA и AB так, что
![]() :
: ![]() =
= ![]() :
: ![]() ,
,
![]() :
: ![]() =
= ![]() :
: ![]() и
и
![]() :
: ![]() =
= ![]() :
: ![]() .
Тогда прямые AA2, BB2 и CC2 либо параллельны, либо также пересекаются в одной
точке Q.
.
Тогда прямые AA2, BB2 и CC2 либо параллельны, либо также пересекаются в одной
точке Q.
В последнем случае точки P и Q называют изотомически
сопряженнымиотносительно треугольника ABC.
(См. задачу 56922.)
Пусть l1, l2 и l3 — соответственные прямые подобных
фигур F1, F2 и F3, пересекающиеся в точке W. Пусть J1, J2 и J3 — точки пересечения
прямых l1, l2 и l3 с окружностью подобия, отличные от точки W. Оказывается,
что эти точки зависят только от фигур F1, F2 и F3 и не
зависят от выбора прямых l1, l2 и l3. Точки J1, J2 и J3
и называют постоянными точками подобных фигур F1, F2 и F3,
а треугольник J1J2J3 называют постоянным треугольником подобных фигур F1, F2 и F3.
(См. задачу 58033.)
Точки A1 и A2 называют соответственными
точками подобных фигур F1 и F2, если при преобразовании подобия, переводящем F1
в F2, точка A1 переходит в A2. Аналогично определяются соответственные прямые и отрезки.
См. также "преобразование подобия".
Трапецией называется четырёхугольник, у которого только две стороны
параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны
называются боковыми сторонами. Параллелограмм не является трапецией по определению.
* Замечательное свойство трапеции: Точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований трапеции лежат на одной прямой. (См. задачу 53749.)
Трапеция с равными боковыми сторонами называется равнобокой.
Равнобокая трапеция обладает следующими свойствами:
* Углы при основании равнобокой трапеции равны. (См. задачу 54149.)
* Диагонали равнобокой трапеции равны и образуют равные углы с основаниями.
* Основание высоты равнобокой трапеции, опущенной из вершины меньшего основания, делит большее основание на отрезки, один из которых равен полусумме оснований, а другой — полуразности. (См. задачу 54158.)
* Около равнобокой трапеции можно описать окружность. (См. задачу 55556.)
Имеют место следующие признаки равнобокой трапеции:
* Если углы при основании трапеции равны, то трапеция равнобокая. (См. задачу 54150.)
* Если диагонали трапеции равны или образуют равные углы с одним из оснований, то трапеция равнобокая.
* Если около трапеции можно описать окружность, то трапеция равнобокая. (См. задачу 55556.)
Треугольником называется фигура, которая состоит из трёх точек,
не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника, а отрезки — сторонами треугольника.
* Против большей стороны треугольника лежит больший угол. (См. задачу 55145.)
* Против большего угла треугольника лежит большая сторона. (См. задачу 55145.)
* Сумма любых двух сторон треугольника больше третьей стороны. (См. "неравенство треугольника".)
* Расстояние между любыми двумя точками, взятыми на сторонах треугольника, не больше наибольшей из его сторон. (См. задачу 55155.)
* Сумма расстояний от произвольной точки внутри треугольника до трёх его вершин больше полупериметра, но меньше периметра треугольника. (См. задачи 55156, 55149.)
* Сумма углов треугольника равна 180o.
* Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним (см. "теорему о внешнем угле треугольника").
* Наибольший угол треугольника не меньше 60o, а наименьший угол треугольника не больше 60o.. (См. задачу 53468.)
см. "точка Брокара".
Прямоугольный треугольник, называется
пифагоровым или египетским, если его стороны,
измеренные в одних и тех же единицах длины, выражаются целыми числами.
Например, трегольники со сторонами (3, 4, 5), (5, 12, 13), (15, 8, 17) — пифагоровы. Если применить к пифагорову треугольнику гомотетию с натуральным коэффициентом, то получится также пифагоров треугольник.
Различных (не подобных) пифагоровых треугольников бесконечно много.
Можно описать все тройки натуральных чисел (x, y, z) такие, что x2 + y2 = z2 следующим образом. Ограничимся случаем взаимно простых чисел x, y, z (все остальные тройки будут пропорциональны данным). Тогда ровно одно из чисел x, y, отвечающих условию x2 + y2 = z2 будет четно. Пусть это y. Тогда необходимо
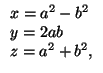
Будем говорить, что точка лежит внутри треугольника, если она принадлежит хотя бы одному отрезку
с концами на треугольнике (то есть с концами на сторонах или в вершинах треугольника). Множество точек,
лежащих внутри треугольника, называется плоским треугольником.
Выражаясь менее формально, плоский треугольник — это внутренняя область треугольника вместе с границей,
а обычный треугольник — это только контур.
Пусть A1, B1 и C1 — основания перпендикуляров, опущенных из
точки P на прямые BC, CA и AB. Треугольник A1B1C1 называют
подерным (или педальным) треугольником
точки P
относительно треугольника ABC. Описанную окружность подерного треугольника
называют подерной (или педальной)
окружностью.
Пусть F1, F2 и F3 — три подобные фигуры, O1 —
центр поворотной гомотетии, переводящей F2 в F3, точки O2
и O3 определяются аналогично. Если точки O1, O2 и O3 не лежат
на одной прямой, то треугольник O1O2O3 называют треугольником
подобия фигур F1, F2 и F3, а его описанную
окружность называют
окружностью подобия этих фигур. В случае, когда
точки O1, O2
и O3 совпадают, окружность подобия вырождается в центр
подобия,
а в случае, когда эти точки не совпадают, но лежат на одной прямой,
окружность подобия вырождается в ось подобия.
См. "постоянные точки".
(См. задачу 58033.)
Треугольник, у которого все стороны равны, называется правильным или
равносторонним.
* Углы равностороннего треугольника равны между собой и равны 60o.
Треугольник называется прямоугольным, если один из его
углов прямой (то есть равен 90o).
Сторона прямоугольного треугольника,
противолежащая прямому углу, называтся гипотенузой, две другие стороны называются катетами.
* Катет прямоугольного треугольника меньше гипотенузы.
* Катет прямоугольного треугольника, лежащий против угла в 30o, равен половине гипотенузы.
* Если катет прямоугольного треугольника равен половине гипотенузы, то он лежит против угла в 30o.
* Угол треугольника при данной вершине является прямым тогда и только тогда, когда медиана, проведенная из этой вершины, равна половине противолежащей стороны.
Имеют место следующие признаки равенства прямоугольных треугольников:
Равнобедренный треугольник обладает следующими свойствами:
* В равнобедренном треугольнике
углы при основании равны (свойство углов равнобедренного треугольника).
* В равнобедренном треугольнике медиана, проведённая к основанию, является
биссектрисой и высотой (свойство медианы равнобедренного треугольника).
* В равнобедренном треугольнике биссектриса, проведённая из вершины, противолежащей
основанию, является медианой и высотой (свойство биссектрисы равнобедренного треугольника).
* В равнобедренном треугольнике высота, проведённая из вершины, противолежащей
основанию, является медианой и биссектрисой (свойство высоты равнобедренного треугольника).
Ниже перечислены некоторые признаки равнобедренного треугольника:
* Если в треугольнике два угла равны,
то он равнобедренный.
* Если высота треугольника является его медианой, то треугольник равнобедренный.
* Если высота треугольника является его биссектрисой, то треугольник равнобедренный.
* Если медиана треугольника является его биссектрисой, то треугольник равнобедренный.
* У подобных треугольников равны соответствующие углы, а соответствующие стороны пропорциональны.
Приведем основные признаки подобия треугольников:
* Если два угла одного треугольника равны двум углам другого, то
такие треугольники подобны.
* Если две стороны одного треугольника пропорциональны двум сторонам
другого и углы, образованные этими сторонами, равны, то треугольники подобны.
* Если стороны одного треугольника пропорциональны сторонам
другого, то треугольники подобны.
* Для подобия прямоугольных треугольников достаточно, чтобы у них было хотя бы по одному равному острому углу.
Равенство
Более коротко, но менее корректно, определение равенства треугольников можно сформулировать так:
* Какой бы ни был треугольник, существует равный ему треугольник в заданном
расположении относительно данной полупрямой (то есть для любого треугольника ABC и
данной полупрямой a с началом в точке A1 существует равный ему треугольник
A1B1C1, вершина B1 которого лежит на полупрямой a, а вершина
C1 расположена в заданной полуплоскости относительно полупрямой a).
Имеют место следующие признаки равенства треугольников:
Если два катета одного прямоугольного треугольника соответственно равны двум катетам
другого, то треугольники равны.
Если катет и прилежащий к нему угол одного прямоугольного треугольника
соответственно равны катету и прилежащему к нему углу другого прямоугольного треугольника, то
треугольники равны.
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету
и гипотенузе другого, то треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны
гипотенузе и острому углу другого, то треугольники равны.
Если катет и противолежащий ему угол одного прямоугольного треугольника
соответственно равны катету и противолежащему ему углу другого прямоугольного треугольника, то
треугольники равны.
Треугольник называется равнобедренным, если у него две стороны равны.
Эти равные стороны называются боковыми сторонами, а третья сторона называется
основанием.
Треугольники называются подобными если они переводятся друг в друга преобразованием подобия. Элементы
данных треугольников, переходящие друг в друга при этом преобразовании, называются соответствующими.
Треугольники называются равными, если существует движение плоскости, переводящее
один треугольник в другой. Элементы равных треугольников (например, вершины, стороны, медианы и т.д.),
переходящие друг в друга при данном движении, называются соответствующими друг другу
или соответственными.
Запись вида
![]() ABC =
ABC = ![]() A1B1C1
означает, что треугольники
ABC и A1B1C1 равны, притом
вершине A соответствует вершина A1, вершине B —
вершина B1, а вершине C — вершина C1.
A1B1C1
означает, что треугольники
ABC и A1B1C1 равны, притом
вершине A соответствует вершина A1, вершине B —
вершина B1, а вершине C — вершина C1.
![]() ABC =
ABC = ![]() A1B1C1
верно тогда и только тогда, когда
A1B1C1
верно тогда и только тогда, когда
![]() ABC =
ABC = ![]() A1B1C1,
A1B1C1, ![]() ACB =
ACB = ![]() A1C1B1,
A1C1B1, ![]() BAC =
BAC = ![]() B1A1C1.
B1A1C1.
Треугольники ABC и
A1B1C1 называются равными, если у
них соответствующие стороны равны и соответствующие углы равны (см. равенства выше).
(признак равенства треугольников по двум сторонам и углу между ними):
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие треугольники равны.
(признак равенства треугольников по стороне и прилежащим к ней углам):
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и
прилежащим к ней углам другого треугольника, то такие треугольники равны.
(признак равенства треугольников по трём сторонам):
Если три стороны одного треугольника соответственно равны трём сторонам
другого треугольника, то такие треугольники равны.
Треугольники ABC и A1B1C1, для которых
перпендикуляры, опущенные из точек A, B, C на прямые B1C1, C1A1, A1B1 пересекаются в одной
точке, называются ортологическими. В этом случае и перпендикуляры, опущенные из точек A1, B1,
C1 на прямые BC, CA, AB также пересекаются в одной точке.
(См. задачу 56955.)
Триссектриссой угла называется луч, проходящий внутри угла и
делящий его на два угла, градусные меры которых относятся в отношении 1 : 2. У каждого угла есть ровно две
триссектрисы, которые делят его на три равные части.
