Статья из журнала "Квант"

В. Я. Березин

Своеобразна судьба иных теорем и задач… Как объяснить, например, столь исключительное внимание со стороны математиков и любителей математики к теореме Пифагора? Почему многие из них не довольствовались уже известными доказательствами, а находили свои, доведя за двадцать пять сравнительно обозримых столетий количество доказательств до нескольких сотен?

Когда речь идет о теореме Пифагора, необычное начинается уже с ее названия. Считается, что сформулировал ее впервые отнюдь не Пифагор. Сомнительным полагают и то, что он дал ее доказательство. Если Пифагор — реальное лицо (некоторые сомневаются даже в этом!), то жил он, скорее всего, в VI-V в. до н. э. Сам он ничего не писал. Называл себя философом, что значило, в его понимании, «стремящийся, к мудрости», основал пифагорейский союз, члены которого занимались музыкой, гимнастикой, математикой, физикой и астрономией. По-видимому, был он и великолепным оратором, о чем свидетельствует следующая легенда, от носящаяся к пребыванию его в городе Кротоне: «Первое появление Пифагора пред народом в Кротоне началось речью к юношам, в которой он так строго, но вместе с тем и так увлекательно изложил обязанности юношей, что старейшие в городе просили не оставить и их без поучения. В этой второй речи он указывал на законность и на чистоту нравов, как на основы семейства; в следующих двух он обратился к детям и женщинам. Последствием последней речи, в которой он особенно порицал роскошь, было то, что в храм Геры доставлены были тысячи драгоценных платьев, ибо ни одна женщина не решалась более показываться в них на улице…» Тем не менее еще во втором столетии нашей эры, т. е. спустя 700 лет, жили и творили вполне реальные люди, незаурядные ученые, находившиеся явно под влиянием пифагорейского союза и относящиеся с большим уважением к тому, что согласно легенде создал Пифагор.

Несомненно также, что интерес к теореме вызывается и тем, что она занимает в математике одно из центральных мест, и удовлетворением авторов доказательств, преодолевших трудности, о которых хорошо сказал живший до нашей эры римский поэт Квинт Гораций Флакк: «Трудно хорошо выразить общеизвестные факты».

Первоначально теорема устанавливала соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника: квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах. Именно в такой формулировке доказывается эта теорема с помощью рисунков, приведенных на первой странице обложки. Здесь на верхнем левом рисунке выделен штриховыми линиями прямоугольный треугольник, на катетах и гипотенузе которого построены квадраты, на гипотенузе — наружу, на катетах — внутрь треугольника. Стороны этих квадратов продолжены везде, где один из квадратов налегает на другой. При этом образовалось несколько треугольников, трапеций и одни голубой квадрат. Равные фигуры окрашены в одинаковый цвет. На тот факт, что треугольник, образованный из красной трапеции и желтого треугольника, равновелик (более того, симметричен) треугольнику, образованному из фиолетового треугольника и зеленой трапеции, обращает внимание фрагмент в правом верхнем углу.

В нижней части рисунка на катетах прямоугольного треугольника (белого) те же самые квадраты построены внешним образом. Попутно в одном из них фиолетово-зеленый треугольник заменен на равновеликий ему красно-желтый. Теперь уже совсем нетрудно показать, что фигура, составленная из двух квадратов, построенных на катетах прямоугольного треугольника, равновелика квадрату, построенному на гипотенузе этого треугольника. Для этого заменяем еще раз зеленую трапецию вместе с фиолетовым треугольником на красную трапецию плюс желтый треугольник и замечаем, что образованная при этом фигура оказывается равносоставленной с квадратом, построенным на гипотенузе данного прямоугольного треугольника. Тем самым доказана и теорема Пифагора.

А вот еще одно доказательство, использующее равносоставленность. На рисунке 1 окрашенный в зеленый цвет отрезок равен одному из катетов, расположенного в нижней части чертежа прямоугольного треугольника, а красный треугольник — равнобедренный и прямоугольный. Доказав, что угол между двумя разрезами — слева и внизу — прямой, усматриваем, как из частей данной фигуры, представляющей собой объединение квадрата н равнобедренного прямоугольного треугольника, можно сложить либо два квадрата, либо один. Причем во втором случае сторона квадрата равняется гипотенузе того самого притаившегося треугольника. Шарнирное крепление на рисунке 2 показывает, что был отрезан прямоугольный треугольник, представляющий половину красного, и повернут относительна «шарнирной» точки на 135^o. На рисунке 3 использованы разрезы рисунка 1. Вновь около шарнирных точек отделенные треугольники поворачиваются на 135^o каждый.

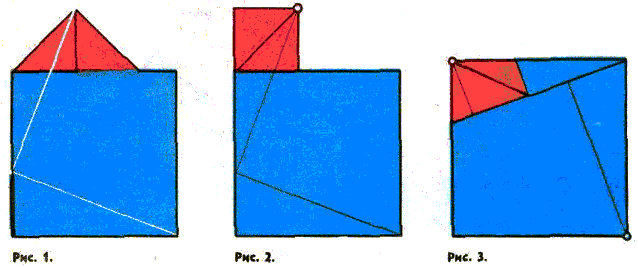
Как проводить доказательство теоремы в случае, когда меньший из катетов более половины большего, вы легко установите сами.

Современная геометрия предпочитает арифметическую формулировку теоремы Пифагора, а именно: если стороны прямоугольного треугольника измерены одним и тем же масштабом, то квадрат числа, выражающего гипотенузу, равен сумме квадратов чисел, выражающих катеты. Коротко: квадрат гипотенузы равен сумме квадратов катетов. Два доказательства, использующих такую формулировку, мы сейчас и проведем.

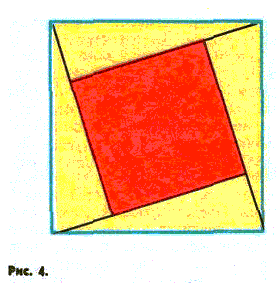
На рисунке 4 изображен квадрат с выделенными на нем четырьмя равными прямоугольными треугольниками. Именно из такого рисунка исходил в своем доказательстве в XII веке индийский математик Бхаскари-Ачарна.

Пусть сторона большого квадрата (она же — гипотенуза прямоугольного треугольника, окрашенного здесь в желтый цвет) равна с. Пусть также два его катета равны соответственно a и b. Тогда, в согласии с чертежом, (a − b)² + (4ab)/2 = с², то есть с² = a² + b². Следовательно, если треугольник прямоугольный, то сумма квадратов его катетов действительно равна квадрату гипотенузы.

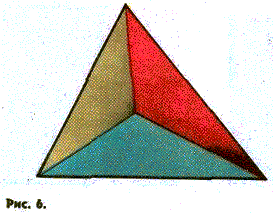
На рисунке 5 один из трех данных прямоугольных треугольников — объемлющий. Все три треугольника — попарно подобные. В этом и ключ к доказательству, ибо площади подобных фигур, построенных соответственно на катетах и гипотенузе данного прямоугольного треугольника, находятся в том же отношении, в каком площади квадратов, построенных на этих катетах и гипотенузе. Иначе говоря, с помощью рисунка мы получаем равенство ka² + k b² = kс², где a и b — катеты объемлющего треугольника, с — его гипотенуза, k — число, равное отношению площади объемлющего треугольника к площади квадрата, построенного на его гипотенузе. Сокращая обе части равенства на k, получаем, как следствие, теорему Пифагора.

Вероятно, за многие столетия со времени открытия теоремы Пифагора немало школьников получило плохие оценки за те или иные ошибки, допущенные при доказательстве. Но, несомненно, более коварной и опасной в этом смысле явилась теорема, ей обратная, на которую в действительности часто надо бы ссылаться в тех случаях, когда школьники ссылаются на теорему Пифагора. Вот формулировка обратной теоремы: если для треугольника со сторонами a, b и с справедливо соотношение a² + b² = с², то треугольник этот — прямоугольный, причем против стороны с находится прямой угол. Доказательство чертежа не требует и проводится очень просто. Действительно, пусть нам дан треугольник, для сторон которого соблюдается соотношение a² + b² = с². Построим теперь прямоугольный треугольник с катетами a и b. Тогда, по прямой теореме Пифагора, гипотенуза этого, построенного нами треугольника будет равняться с = √(a² + b²). Следовательно, он будет равен по трем сторонам данному треугольнику, который поэтому должен быть прямоугольным.

Приведем теперь два обобщения теоремы Пифагора.

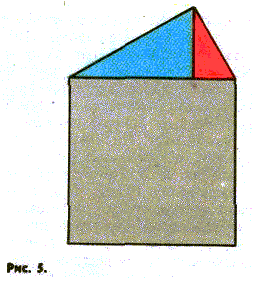
Первое — стереометрическое. Оно установлено впервые, по-видимому, в XVII столетии и довольно часто встречается в прикладной математике. Оказывается, что сумма квадратов площадей трех прямоугольных треугольников, являющихся гранями тетраэдра и имеющих общую вершину при прямых углах (рис. 6), равна квадрату площади невидимой грани этого тетраэдра. Доказательство указанного факта предлагается вам провести самостоятельно.

Второе обобщение — теорема Паппа Александрийского (III век н. э.). Она гласит: во всяком треугольнике параллелограмм, построенный на одной стороне треугольника внутрь его и имеющий две другие вершины вне треугольника, равновелик сумме двух параллелограммов, построенных на двух других сторонах треугольника так, что стороны их, параллельные сторонам треугольника, проходят через вершины первого параллелограмма. Короче говоря, на рисунке 7 площадь нижнего параллелограмма равна сумме площадей параллелограммов, построенных на боковых сторонах треугольника.

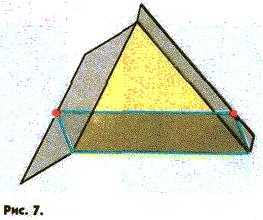
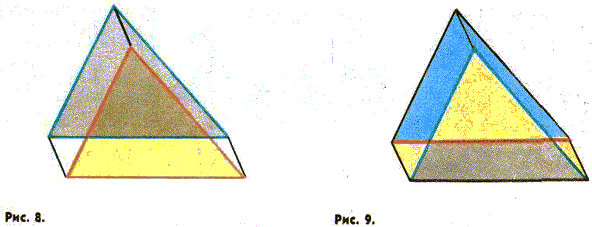
На рисунке 8 отчетливо выделяются два равных, а потому и равновеликих треугольника с параллельными соответственными сторонами. На рисунке 9 выделены две трапеции на боковых, сторонах данного треугольника, сумма площадей которых равна площади трапеции, построенной на его основании. Отсюда сразу следует справедливость теоремы Паппа. Много доказательств теоремы Пифагора, некоторые из которых исключительно изящны, вы можете найти в книге В. Литцмана «Теорема Пифагора». О самом Пифагоре рассказывается в книге Б. Л. Ван-дер-Вардена «Пробуждающаяся наука».

ДОКАЗАТЕЛЬСТВО В КАРТИНКАХ

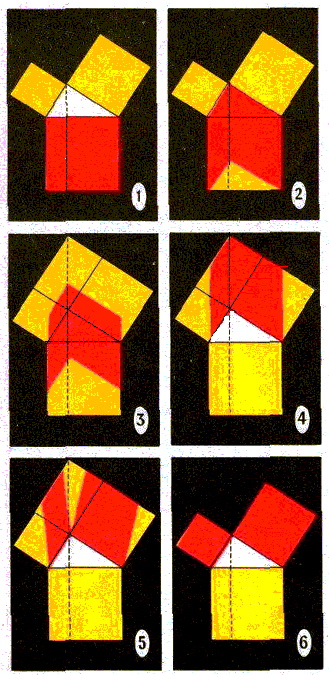
На рисунках запечатлены последовательные этапы доказательства теоремы Пифагора. Красной краски, затраченной на то, чтобы покрасить квадрат, построенный на гипотенузе прямоугольного треугольника (рис. 1), оказывается равно столько, сколько ее требуется, чтобы покрасить квадраты, построенные на катетах этого треугольника (рис. 6). На рисунке 2 квадрат превратился а равновеликую ему фигуру, по форме напоминающую развернутую книгу, движущуюся затем вверх.

Тот факт, что продолженная на рисунке 3 пунктиром высота прямоугольного треугольника попадает в точку пересечения продолжений сторон квадратов, построенных на катетах, требует обосновании — оно приведено на второй странице обложки. На следующих рисунках «книжка» распадается на параллелограммы, а они превращаются в равновеликие им квадраты, построенные на катетах данного прямоугольного треугольника. Тем самым сумма площадей квадратов, построенных на катетах произвольного прямоугольного треугольника, оказывается равной площади квадрата, построенного на его гипотенузе. Теорема Пифагора доказана.