А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'Б':
Биссектрисой угла называется луч, который проходит между сторонами угла и
делит угол пополам.
* Биссектриса угла есть геометрическое место точек, лежащих внутри угла и равноудаленных от его сторон.
Биссектрисой треугольника, проведенной из данной вершины, называется
отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на
противоположной стороне.
* Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности данного треугольника.
* Биссектриса треугольника делит его сторону на отрезки, пропорциональные
двум другим сторонам, то есть,
если D — точка пересечения биссектрисы угла C
со стороной AB треугольника ABC, то
![]() =
= ![]() .
(См. задачу 53745.)
.
(См. задачу 53745.)
* Если биссектриса внешнего угла треугольника пересекает противоположную сторону,
то она делит ее внешним образом на отрезки, пропорциональные двум другим сторонам, то есть,
если биссектриса угла, смежного с углом C
пересекает продолжение стороны AB треугольника ABC в точке
D, то
![]() =
= ![]() .
(См. задачу 53880.)
.
(См. задачу 53880.)
Отметим, что биссектриса
внешнего угла может и не пересекать противоположную сторону (в случае равнобедренного треугольника).
* Если биссектрисы углов A и B треугольника ABC пересекаются в
точке O, то
![]() AOB = 90o + 1/2
AOB = 90o + 1/2![]() C.
C.
* Квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой, то есть
* Если lc — биссектриса треугольника, проведённая из вершины угла,
равного ![]() , заключённого между сторонами a и b, то
, заключённого между сторонами a и b, то
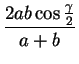 .
.
(См. задачу 55274.)
* Если lc — биссектриса треугольника со сторонами a, b и c, то
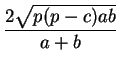 ,
,
