А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'Ф':
Факториалом натурального числа n при n>1 называется
произведение всех последовательных натуральных чисел от 1 до n
включительно. Факториал обозначается восклицательным знаком:
n!=1.2.....n.
Например, 2!=2, 3!=6, 5!=120.
По определению полагают также, что 1!=1 и 0!=0.
* n! — это количество различных перестановок из n элементов.
В планиметрии (стереометрии) принято называть фигурой произвольное подмножество
плоскости (пространства). Таким образом, по сложившейся традиции в классической геометрии
слово "фигура" употребляется вместо слова "множество". Отметим при этом, что
равенство фигур не означает совпадения множеств, а определяется отдельно
(см. "равные фигуры"). Ранее существовал термин "конгруэнтность",
позволявший отличать равенство фигур в смысле приведенного ниже определения от совпадения фигур как множеств.
Но, в силу различных причин этот термин в настоящее время больше не является общеупотребительным.
Фигуру называют выпуклой, если любой отрезок
с концами в точках фигуры целиком принадлежит ей.
Две фигуры на плоскости (в пространстве) называются подобными, если существует преобразование
подобия, взаимно однозначно переводящее одну фигуру в другую.
Элементы данных фигур, переходящие друг в друга при этом преобразовании подобия, называются соответствующими
или соответственными.
* Каждая фигура подобна самой себе.
* Равные фигуры подобны.
* Если фигура F1 подобна фигуре F2 с коэффициентом k, то фигура F2 подобна
фигуре F1 с коэффциентом
![]() .
.
* Если фигура F1 подобна фигуре F2 с коэффициентом k1, а фигура F2 подобна фигуре F3 с коэффициентом k2, то фигура F1 подобна фигуре F3 с коэффициентом k1k2.
* У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если треугольники ABC и A1B1C1 подобны, то
![]() A =
A = ![]() A1,
A1, ![]() B =
B = ![]() B1,
B1, ![]() C =
C = ![]() C1,
C1, 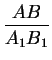 =
= 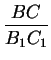 =
= 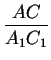 .
.
* Отношение площадей подобных фигур равно квадрату коэффициента подобия, а отношение объемов подобных фигур равно кубу коэффициента подобия.
Простой фигурой или простой многоугольной фигурой на плоскости называется объединение конечного числа
плоских треугольников, любые два из которых либо не имеют ни одной общей точки,
либо имеют одну и только одну общую вершину, либо одну и только одну общую сторону.
Две фигуры называются на плоскости (в пространстве) называются равновеликими, если их площади
(объемы) равны.
* Любые две простые равновеликие фигуры на плоскости (в том числе, например, равновеликие многоугольники) равносоставлены. (Теорема Больяи-Гервина).
* Неверно, что любые две равновеликие многогранные фигуры в пространстве равносоставлены. Контрпримером могут служить правильный тетраэдр и куб одного объема. (Теорема Дена)
Две простые многоугольные фигуры на плоскости называются
равносоставлеными, если каждую из них можно разбить на конечное (одно и то же для обеих фигур) число простых
многоугольных фигур M1,M2,...,Mn и M'1,
M'2,...,M'n соответственно, так, что при всех k фигуры Mk
и M'k равны (то есть совмещаются движением). При этом мы называем фигуру разбитой
на несколько частей (простых фигур), если объединение этих частей совпадает с данной фигурой, а попарные пересечения
частей либо пусты, либо состоят из объединения конечного числа точек и отрезков.
Аналогично можно дать определение равновеликих
простых многогранных фигур в пространстве, при этом от частей, на которые разбита такая фигура, достаточно потребовать, чтобы
их пересечение было либо пусто, либо состояло из объединения конечного числа точек, отрезков и простых многоугольных фигур.
* Любые две равносоставленные фигуры равновелики.
* Любые две простые равновеликие фигуры на плоскости (в том числе, например, равновеликие многоугольники) равносоставлены. (Теорема Больяи-Гервина).
* Любые две простые равновеликие фигуры на плоскости можно так разбить на равные части, что соответствующие части можно будет совместить только с помощью параллельных переносов и центральных симметрий (теорема Хадвигера-Хлюра). В частности, две равновеликие простые многоугольные фигуры всегда можно разбить на части (на простые многоугольные фигуры) с соответственно параллельными сторонами.
* Неверно, что любые две равновеликие многогранные фигуры в пространстве равносоставлены. Контрпримером могут служить правильный тетраэдр и куб одного объема. (Теорема Дена)
* Третья проблема Гильберта ставит вопрос, верно ли, что любые два тетраэдра с равными основаниями и равными высотами равносоставлены (или хотя бы дополняемы равными частями до равносоставленных многогранников)? Ответ на этот вопрос отрицателен. Тем самым неверно и то, что всякий тетраэдр равносоставлен с некоторым прямоугольным параллелепипедом (хотя некоторые такие тетраэдры существуют).
Две фигуры на плоскости (в пространстве) называются равными, если существует движение, взаимно однозначно переводящее одну фигуру в другую.
Элементы данных фигур (вершины, стороны, центры и т.д.), переходящие друг в друга при этом движении, называются соответствующими
друг другу или соответственными.
* Если фигура F1 равна фигуре F2, а фигура F2 равна фигуре F3, то фигуры F1 и F3 равны.
* У равных фигур равны величины соответствующих углов, и длины соответствующих отрезков.
* Равные фигуры имеют одинаковую площадь.
см. "гипербола".
см. "парабола".
Если a, b, c, d — стороны вписанного четырёхугольника, p —
его полупериметр, а S — площадь, то
(См. задачу 53061.)
Площадь треугольника можно вычислить по формуле
S = ![]() , где а, b,с — стороны, а р — полупериметр данного треугольника.
Данная формула называется формулой Герона.
, где а, b,с — стороны, а р — полупериметр данного треугольника.
Данная формула называется формулой Герона.
(См. задачу 57600.)
Рассмотрим многоугольник (не обязательно выпуклый) с вершинами в узлах
целочисленной решетки. Его площадь можно вычислить по формуле Пика: S = n + m/2 - 1,
где n — число узлов решетки, лежащих строго внутри (не на границе) данного многоугольника, а
m — число узлов, лежащих на его границе.
(См. задачу 58208.)
Есть много формул, по праву носящих имя великого математика Леонарда Эйлера
(4(15).4.1707, Базель, Швейцария, - 7(18).9.1783, Петербург). Приведем некоторые из них:
—
ei![]() = cos
= cos![]() + i sin
+ i sin![]() .
.
—
![]() =
= ![]() (1 -
(1 - ![]() ). Одним из следствий этой формулы является равенство
1 +
). Одним из следствий этой формулы является равенство
1 + ![]() +
+ ![]() +
+ ![]() + ... =
+ ... = ![]() .
.
— о простых числах:
![]()
![]() =
= ![]() 1/(1 - p-s), где в правой части формулы произведение
берется по всем натуральным простым числам p.
1/(1 - p-s), где в правой части формулы произведение
берется по всем натуральным простым числам p.
