А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'П':
Есть несколько эквивалентных определений параболы:
— Параболой называется график функции y = ax2 (при a![]() 0) в некоторой прямоугольной системе координат.
0) в некоторой прямоугольной системе координат.
* График любого квадратного трехчлена
y = ax2 + bx + c (a![]() 0)
является параболой, так как он получается из графика функции y = ax2 с помощью параллельного переноса
(выделение полного квадрата).
0)
является параболой, так как он получается из графика функции y = ax2 с помощью параллельного переноса
(выделение полного квадрата).
* Таким образом, все параболы подобны.
— Параболой называется множество точек плоскости, которое в некоторой прямоугольной системе
координат задается уравнением y2 = 2px при p![]() 0. Данное уравнение называется
каноническим уравнением параболы. Точку (0, p/2) называют
фокусом параболы, а прямую y = - p/2 —
директрисой параболы.
0. Данное уравнение называется
каноническим уравнением параболы. Точку (0, p/2) называют
фокусом параболы, а прямую y = - p/2 —
директрисой параболы.
* Расстояние от любой точки параболы до фокуса равно расстоянию от этой точки до директрисы параболы.
— Параболой называется геометрическое место точек, для которых расстояния до некоторой
фиксированной точки (называемой фокусом) и до некоторой фиксированной прямой
(директрисой) равны.
* Парабола является коническим сечением, то есть она может быть получен как сечение конуса подходящей плоскостью.
* Параболическое зеркало обладает тем свойством, что лучи света, идущие внутри параболы параллльно ее оси, после первого отражения концентрируются в ее фокусе. Или, что то же самое, если поместить источник света в фокусе параболы, то после отражения получится пучок лучей, параллельных оси параболы.
Параллелограммом называется четырёхугольник, у которого противолежащие
стороны попарно параллельны, то есть лежат на параллельных прямых. Центром параллелограмма называется точка пересечения его диагоналей.
Параллелограмм обладает следующими свойствами:
* Диагональ разбивает параллелограмм на два равных треугольника.
* Противолежащие стороны параллелограмма попарно параллельны.
* Противолежащие углы параллелограмма попарно равны, а сумма углов, прилежащих к одной стороне, равна 180o.
* Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
Имеют место следующие признаки параллелограмма:
* Если противолежащие стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
* Если противолежащие углы четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
* Если две противолежащие стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
* Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Также верны следующие утверждения:
* Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон, то есть, если a и b — соседние стороны параллелограмма, а d1 и d2 — диагонали, то
- Вариньона
Середины сторон любого четырёхугольника являются вершинами параллелограмма, который называется (параллелограммом Вариньона). (См. задачу 53475.)
* Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырехугольника.
* Если четырехугольник выпуклый, то площадь его параллелограмма Вариньона равна половине площади исходного четырехугольника. (См. задачу 54963.)
Параллельным переносом
на вектор
![]() называют преобразование плоскости (пространства),
переводящее точку X в такую точку X', что
называют преобразование плоскости (пространства),
переводящее точку X в такую точку X', что
![]() =
= ![]() .
.
Рассмотрим фигуры, ограниченные гладкими или
кусочно-гладкими кривыми. Периметром такой фигуры называют длину кривой,
ограничивающей эту фигуру. В частности, периметр многоугольника — это сумма длин его сторон.
* Если один выпуклый плоский многоугольник расположен внутри другого, то периметр первого не превосходит периметр второго. В случае невыпуклых многоугольников это неверно.
Пусть точка A не лежит на прямой b, а прямая a, перпендикулярная b,
проходит через точку A и пересекает прямую b в точке B. Тогда отрезок AB называется
перпендикуляром, опущенным из точки A на прямую b.
Если точка A лежит на прямой b, то отрезок AB прямой, перпендикулярной b, называется
перпендикуляром, восставленным (или восстановленным) из точки A к прямой b.
Конец перпендикуляра, принадлежащий прямой b, называется основанием перпендикуляра.
* Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
См. статью
"площадь" из Энциклопедии элементарной математики.
см. "преобразование подобия".
см. "луч".
Если точка P лежит вне окружности S, а PA и PB — касательные
к окружности, то прямую AB называют полярой точки P
относительно окружности S.
Рассмотрим цепочку окружностей
S1, S2,..., Sn, каждая из которых касается двух соседних
(Sn касается Sn - 1 и S1) и двух данных непересекающихся
окружностей R1 и R2. Тогда для любой окружности T1, касающейся R1 и R2
(одинаковым образом, если R1 и R2 не лежат одна в другой,
внешним и внутренним образом — в противном случае), существует
аналогичная цепочка из n касающихся окружностей
T1, T2,..., Tn. Этот факт и называется
поризмом Штейнера.
(См. задачу 58357.)
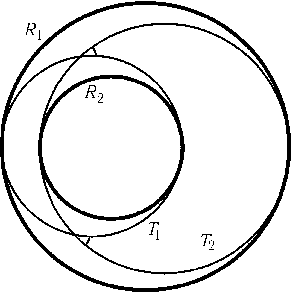
Последовательность чисел
a0, a1, ..., an,... , которая при
заданных b0, b1, ...,bk-1
удовлетворяет соотношениям
называется линейной рекуррентной последовательностью k-го порядка.
Уравнение
называется характеристическим уравнением последовательности {an}.
Последовательностью Фарея Fn называют возрастающую последовательность
несократимых дробей a/b, где
a, b ![]()
![]() ,
0 < a < b
,
0 < a < b![]() n.
n.
*
Если a/b и c/d — соседние члены последовательности Фарея, то
| ad - bc| = 1.
(См. задачу 58209.)
Правилом треугольника — называется следующая теорема о сложении векторов, верная как на плоскости так и в пространстве:
Для любых трёх точек A, B и
C верно равенство
![]() +
+ ![]() =
= ![]() .
.
Правило треугольника имеет очевидный физический смысл: композиция (последовательное выполнение) перемещений из A в B и из B в C совпадает с перемещением из A в C.
Правилом параллелограмма — называется следующая теорема о сложении векторов, верная как на плоскости так и в пространстве:
Для любых трёх точек A, B и C, не лежащих на одной прямой,
сумма векторов
![]() и
и
![]() есть вектор
есть вектор
![]() , где точка D — вершина параллелограмма ABDC.
, где точка D — вершина параллелограмма ABDC.
Преобразование плоскости называется аффинным, если оно
взаимно однозначно, и образом любой прямой является прямая.
*
Аффинное преобразование является непрерывным преобразованием плоскости.
(См. задачу 58377.)
* Отметим, что взаимно однозначное отображение плоскости в себя,
переводящее любую окружность в окружность, является аффинным преобразованием плоскости.
(См. задачу 58378.)
*
Частным случаем аффинных преобразований являются движения
и преобразования подобия.
(См. задачи 58368,58371.)
См. "дробно-линейные преобразования".
Преобразование фигуры F в фигуру F' (на плоскости или в пространстве) называется преобразованием
подобия, если при этом преобразовании расстояния между точками умножается на одно и то же положительное число k,
называемое коэффициентом подобия, то есть если для произвольных точек X и Y фигуры F и их образов
X' и Y', принадлежащих фигуре F', выполняется равенство
X'Y' = k . XY.
Две фигуры на плоскости (в пространстве) называются подобными, если существует преобразование подобия, взаимно однозначно переводящее одну фигуру в другую.
* Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки.
* Преобразование подобия переводит окружности в окружности.
* Преобразование подобия сохраняет углы между лучами и углы между окружностями; в частности преобразование подобия сохраняет касание.
Отображение P плоскости ![]() на плоскость
на плоскость ![]() называют проективным, если оно является композицией центральных
проектирований и аффинных преобразований, то есть если
существуют плоскости
называют проективным, если оно является композицией центральных
проектирований и аффинных преобразований, то есть если
существуют плоскости
![]() =
= ![]() ,
,
![]() ,...,
,...,![]() =
= ![]() и отображения Pi плоскостей
и отображения Pi плоскостей ![]() на
на
![]() , каждое из
которых является либо центральным проектированием, либо аффинным
преобразованием, причем P является композицией преобразований Pi.
В случае, когда плоскость
, каждое из
которых является либо центральным проектированием, либо аффинным
преобразованием, причем P является композицией преобразований Pi.
В случае, когда плоскость ![]() совпадает с плоскостью
совпадает с плоскостью ![]() ,
отображение P называют проективным преобразованием
плоскости
,
отображение P называют проективным преобразованием
плоскости ![]() .
Прообраз бесконечно удаленной прямой называется
исключительной прямой данного проективного преобразования.
.
Прообраз бесконечно удаленной прямой называется
исключительной прямой данного проективного преобразования.
— Пусть l1 и l2 — две прямые на плоскости,
O — точка, не лежащая ни на одной из этих прямых. Центральным
проектированием прямой l1 на прямую l2
с центром O называют
отображение, которое точке A1 прямой l1 ставит в соответствие
точку пересечения прямой OA1 с прямой l2.
— Пусть ![]() и
и ![]() — две плоскости в пространстве,
O — точка, не лежащая ни на одной из этих плоскостей.
Центральным проектированием
плоскости
— две плоскости в пространстве,
O — точка, не лежащая ни на одной из этих плоскостей.
Центральным проектированием
плоскости ![]() на плоскость
на плоскость ![]() с центром O называют отображение, которое точке A1 плоскости
с центром O называют отображение, которое точке A1 плоскости ![]() ставит в соответствие точку пересечения прямой OA1 с плоскостью
ставит в соответствие точку пересечения прямой OA1 с плоскостью ![]() .
.
Пусть l1 и l2 — две прямые на плоскости, l —
прямая, не параллельная ни одной из этих прямых. Параллельным
проектированием прямой l1 на прямую l2
вдоль прямой l называют
отображение, которое точке A1 прямой l1 ставит в соответствие
точку пересечения прямой l2 с прямой, проходящей через точку A1
параллельно прямой l.
см. "стереографическая проекция".
Псевдоскалярным произведением
ненулевых векторов
a и
b называют число
c = |a| . |b| sin![]() (a,b);
если хотя бы один из векторов
a и
b
нулевой, то c = 0. Число c обозначается через
a
(a,b);
если хотя бы один из векторов
a и
b
нулевой, то c = 0. Число c обозначается через
a ![]() b.
Ясно, что
a
b.
Ясно, что
a ![]() b = - b
b = - b ![]() a.
a.
Абсолютная величина псевдоскалярного произведения векторов
a
и
b равна площади параллелограмма, натянутого на эти векторы.
В связи с этим ориентированной площадью
тройки точек A, B и C
называют число
S(A, B, C) = (![]()
![]()
![]() )/2; абсолютная
величина числа S(A, B, C) равна площади треугольника ABC.
)/2; абсолютная
величина числа S(A, B, C) равна площади треугольника ABC.
Скалярное произведение обладает следующими свойствами:
*
(a,b) = (b,a);
*
|(a,b)|
*
(
*
если
a,b
* Если в некоторой прямоугольной системе координат векторы имеют координаты
a = (a1, a2,..., an),
b = (b1, b2,..., bn), то скалярное произведение можно вычислить
по следующей формуле:
(a,b) = a1b1 + a2b2 + ... + bnyn. В частности, для векторов
на плоскости
a = (x1, y1),
b = (x2, y2) скалярное произведение вычисляется по
формуле
(a,b) = x1x2 + y1y2.
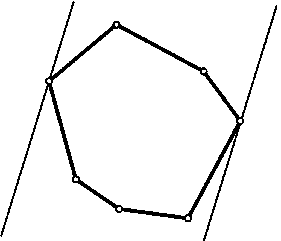
* Для любого выпуклого многоугольника существуют ровно две
опорные прямые, параллельные данной прямой.
Открытие этой прямой
долго приписывалось Роберту Симсону (1687-1768), но в действительности она
была открыта лишь в 1797 году Вильямом Уоллесом. Поэтому наряду с традиционным
названием этой прямой часто используется исторически более справедливое
название прямая Уоллеса.
* Отметим, что точка M лежит на отрезке OH, причем OM : MH = 1 : 2.
* Через точку, не лежащую на прямой, можно провести параллельную ей прямую, и
только одну.
* Две различные прямые, параллельные третьей, параллельны.
* Если прямая (на плоскости) пересекает одну из двух параллельных прямых (и не совпадает с ней),
то она пересекает и другую прямую.
* Две различные прямые (на плоскости), перпендикулярные третьей, параллельны.
* Если две параллельные прямые пересечены третьей прямой, то внутренние накрест
лежащие углы равны, а сумма внутренних односторонних углов равна
180o.
* Если внутренние накрест лежащие углы равны или сумма внутренних односторонних
углов равна
180o, то прямые параллельны.
* Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна
и другой.
*
На плоскости через каждую точку, лежащую на прямой, можно провести перпендикулярную ей прямую,
и притом только одну.
* Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна
и другой.
* Диагонали прямоугольника равны.
* Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Скалярным произведением векторов
a и
b называют число
(a,b) = | a| . | b| cos![]() (a,b)
(если один из этих векторов нулевой, то
(a,b) = 0 по определению).
(a,b)
(если один из этих векторов нулевой, то
(a,b) = 0 по определению).
![]() |a| . |b|;
|a| . |b|;
![]() a +
a + ![]() b,c) =
b,c) = ![]() (a,c) +
(a,c) + ![]() (b,c);
(b,c);
![]() 0, то
(a,b) = 0
тогда и только тогда, когда
a
0, то
(a,b) = 0
тогда и только тогда, когда
a ![]() b.
b.
См. статью
"производная" из Энциклопедии элементарной математики.
Если никакие стороны четырехугольника
не параллельны, то середина отрезка, соединяющего
точки пересечения противоположных сторон, лежит на прямой, соединяющей
середины диагоналей. Эта прямая называется прямой Гаусса.
(См. задачу 56806.)
См. "преобразования проективные".
Опорной прямой выпуклого многоугольника называют
прямую, проходящую через его вершину и обладающую тем свойством, что
многоугольник лежит по одну сторону от нее.
Основания перпендикуляров, опущенных
из точки описанной окружности треугольника на его стороны или их
продолжения, лежат на одной прямой. Эта прямая называется
прямой Симсона.
(См. задачу 52421.)
См. "прямая Симсона".
Пусть H — точка пересечения высот
треугольника ABC, O — центр описанной окружности, M — точка
пересечения медиан. Точки M, H и O лежат на одной прямой,
которую называют прямой Эйлера.
см. задачу 56957
Две прямые на плоскости называются параллельными, если они не имеют ни одной
общей точки.
Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым
углом, то есть один (а значит, каждый) из вертикальных углов, образованных этими прямыми,
равен 90o.
Прямоугольником называется параллелограмм, у которого все углы прямые.
