А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'Д':
Движением называют преобразование плоскости (пространства или фигуры на плоскости или в пространстве), сохраняющее расстояния
между точками, то есть если A' и B' — образы точек A и B
при движении, то A'B' = AB.
* Композиция движений является также движением.
* Преобразование, обратное движению, также является движением.
* При движении прямые переходят в прямые, полупрямые — в полупрямые, а отрезки — в отрезки.
* При движении окружности переходят в окружности.
* Движение сохраняет углы между лучами (угол переходит в равный ему угол) и углы между окружностями. В частности, движение сохраняет касание.
См. также раздел "теорема Шаля".
— Двойным отношением четверки точек A, B, C, D,
лежащих на одной прямой, называют число
* Двойное отношение четверки точек сохраняется при проективных преобразованиях.
см. задачу 58410
— Двойным отношением четверки прямых a, b,
c, d,
проходящих через одну точку, называют число
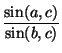 :
: 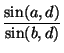 ,
,
Диаграммой Юнга, соответствующей показателю α=(α1, α2, ..., αn) называется лестница из n ступенек, у которой высота k-ой ступеньки равна αk, а ширина — единице.
Число α1+α2+...+αn называется весом диаграммы Юнга.
Говорят, что диаграмма Юнга, соответствующая набору α=(α1, α2, ... , αn), мажорирует диаграмму Юнга, соответствующую набору β=(β1, β2, ... , βn), если справедлива система неравенств:
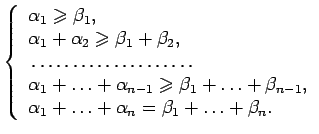
В этом случае также говорят, что набор α мажорирует набор β, и записывают это как
Диаметром окружности называется
хорда данной окружности, проходящая через ее центр.
* Диаметр, перпендикулярный хорде, делит её пополам. (См. задачу 53911.)
* Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде. (См. задачу 53912.)
* Серединный перпендикуляр к хорде проходит через центр окружности.
Диаметром Брокара называют диаметр окружности Брокара
Диаметром гиперболы называют произвольную
хорду, проходящую через её центр. Сопряжёнными диаметрами гиперболы
называют пару её диаметров,
обладающих следующим свойством: середины хорд, параллельных первому диаметру,
лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру,
лежат на первом диаметре.
Диаметром эллипса называют произвольную хорду,
проходящую через его центр. Сопряжёнными диаметрами
эллипса называют пару его диаметров,
обладающих следующим свойством: середины хорд, параллельных первому диаметру,
лежат на втором диаметре. В этом случае и
середины хорд, параллельных второму диаметру, лежат на первом диаметре.
*
Если эллипс является образом окружности при аффинном преобразовании, то его
сопряжённые диаметры являются образами двух перпендикулярных диаметров
этой окружности.
(См. задачу 58474.)
см. "гипербола".
см. "парабола".
Преобразования (расширенной) комплексной плоскости
вида
z![]()
![]() , где
a, b, c, d
, где
a, b, c, d ![]()
![]() ,
ad - bc
,
ad - bc![]() 0, называются дробно-линейными преобразованиями (отображениями).
0, называются дробно-линейными преобразованиями (отображениями).
Можно также рассматривать и дробно-линейные преобразования (проективной) вещественной прямой:
x![]()
![]() , где
a, b, c, d
, где
a, b, c, d ![]()
![]() ,
ad - bc
,
ad - bc![]() 0.
0.
* Отметим, что преобразование вещественной прямой является проективным тогда и только тогда, когда оно
дробно-линейно.
Пересечение окружности и (плоского) центрального угла данной окружности называется дугой
окружности, соответствующей данному центральному углу. Градусной мерой дуги окружности называется градусная мера соответствующего
центрального угла.
