А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'Н':
Пусть BA — перпендикуляр, опущенный из точки B на прямую a,
C — любая точка прямой a, отличная от A. Отрезок BC называется наклонной,
проведённой из точки B к прямой a. Точка C называется основанием наклонной.
Отрезок AC называется (ортогональной) проекцией наклонной.
* Если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные (ортогональные) проекции, из двух наклонных больше та, проекция которой больше.
Неравенство Йиффа утверждает, что для угла Брокара ![]() данного
треугольника выполнено неравенство
8
данного
треугольника выполнено неравенство
8![]()
![]()
![]()
![]()
![]() ,
где
,
где
![]() ,
,![]() ,
,![]() — углы искомого треугольника.
— углы искомого треугольника.
(См. задачу 56975.)
Для любых неотрицательных чисел
x1, x2,..., xn верно неравенство:
(См. задачу 60310.)
Пусть a, b, c и a', b', c' — длины сторон треугольников ABC и
A'B'C', S и S' — их площади. Тогда
(См. задачу 57466.)
Для любых точек A, B, C, D плоскости выполнено неравенство
Неравенства Птолемея можно распространить и на шесть точек: если A1, A2, ...A6 — произвольные точки плоскости, то
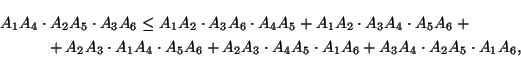
причем равенство достигается тогда и только тогда, когда
A1...A6 — вписанный шестиугольник.
(См. задачу 58396.)
Неравенство треугольника утверждает, что для любых трех точек A, B, C плоскости (пространства) верно, что
| AB| + | BC| ![]() | AC|,
где через | XY| обозначено расстояние между точками X и Y.
| AC|,
где через | XY| обозначено расстояние между точками X и Y.
* Неравенство треугольника обращается в равенство тогда и только тогда, когда точки A, B и C лежат на одной прямой, причем B лежит между A и C.
* Если
![]() ,
,![]() — два вектора (два элемента нормированного пространства),
то неравенство треугольника примет вид
|
— два вектора (два элемента нормированного пространства),
то неравенство треугольника примет вид
|![]() | + |
| + |![]() |
| ![]() |
|![]() |, где через
|
|, где через
|![]() | обозначена длина (норма) вектора
| обозначена длина (норма) вектора
![]() . Неравенство обращается в равенство тогда
и только тогда, когда векторы
. Неравенство обращается в равенство тогда
и только тогда, когда векторы
![]() и
и
![]() сонаправлены.
сонаправлены.
Длина ломаной (на плоскости или в пространстве) не меньше длины отрезка, соединяющего её концы.
Пусть точка O лежит внутри треугольника ABC. Обозначим
расстояния от точки O до сторон BC, CA, AB треугольника через
da, db, dc,
а расстояния от точки O до вершин A, B, C через
Ra, Rb, Rc. Тогда
(См. задачу 56810.)
