В этом кратком справочнике поясняются понятия и теоремы, упоминаемые в книгах и задачах, опубликованных на нашем сайте. Справочник ни в кой мере претендует на полноту — это лишь необходимый комментарий к нашим задачам. Справочник формируется в соответствии с запросами наших читателей. Если Вас интересует, что означает данный термин, или что утверждает данная теорема, заполните форму, и мы ответим на Ваш вопрос.

Запрос

От кого (e-mail):
Что Вас интересует:

Знаком "*" помечены факты, относящиеся к данному понятию, знаком "-" помечены варианты формулировки определений.

А  Б  В  Г  Д  З  И  К  Л  М  Н  О  П  Р  С  Т  У  Ф  Х  Ц  Ч  Э  

Статьи на букву 'Г':

• Гипербола
  Есть несколько эквивалентных определений гиперболы:

  
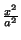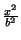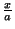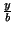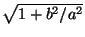  —  Гиперболой называется множество точек плоскости, которое в некоторой прямоугольной системе координат задается уравнением - = 1. Данное уравнение называется каноническим уравнением гиперболы. Прямые = ± называют асимптотами гиперболы. Число e = называют эксцентриситетом, а прямые x = ±a/e называют директрисами гиперболы.

  
  —  Гиперболой называется геометрическое место точек, разность расстояний от которых до двух заданных точек F₁ и F₂ есть постоянная (положительная) величина.

  Точки F₁ и F₂ называют фокусами гиперболы.

  *  Отношение расстояния от точки гиперболы до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету гиперболы e.

  Верно и обратное: если дана точка F и прямая l, не содержащая F, то множество точек X, для которых отношение расстояния от X до F к расстоянию от X до l равно постоянному числу числу e > 1, является гиперболой.

  *  Гипербола является коническим сечением, то есть может быть получена как сечение конуса подходящей плоскостью.

  • Енжабека
    Кривую, изогонально сопряженную прямой Эйлера, называют гиперболой Енжабека.
  • Киперта
    Кривую, изогонально сопряженную прямой OK, где K — точка Лемуана, а O — центр описанной окружности данного треугольника, называют гиперболой Киперта
  • равнобочная (равнобедренная)
    Гиперболу, которую можно в некоторой прямоугольной системе координат задать уравнением y = 1/x, называют равнобочной.

    *  Произвольная гипербола получается из равнобочной гиперболы аффинным преобразованием.

  
  (См. задачи 58513,58516.)

• Гипотенуза
  см. "треугольник прямоугольный".

• Гомотетия
  Гомотетией c центром O и коэффициентом k (k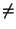 0) называют преобразование плоскости (пространства), переводящее точку X в точку X', обладающую тем свойством, что 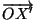= k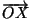. Иногда в определении гомотетии требуют положительности коэффицента гомотетии, но таким определением менее удобно пользоваться при решении задач.

  Гомотетию с центром O и коэффициентом k часто обозначают через H_O^k.

  • Поворотная гомотетия
    Поворотной гомотетией называют композицию гомотетии и поворота, имеющих общий центр. Порядок, в каком берется композиция, несуществен, так как R_O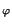oH_O^k = H_O^koR_O.

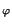    *  Коэффициент поворотной гомотетии можно считать положительным, так как R_O^180ooH_O^k = H_O^-k.